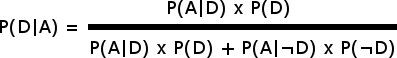Probabilidade e algumas aplicações em Python
April 19, 2016
Introdução
Seguindo a linha do último post sobre Estatística, este post será uma introdução ao mundo da Probabilidade, apresentando alguns dos principais conceitos do assunto e como podemos fazer os cálculos relativos utilizando Python.
Probabilidade é a medida numérica que representa a chance de um determinado evento acontecer. Qual é a chance de eu jogar um dado e tirar um número 6? De eu jogar duas moedas para cima e as duas resultarem em Coroa? Essas perguntas (e muitas outras) são respondidas pela Probabilidade.
Para o cálculo básico da probabilidade de um evento, somamos todas as possibilidades que atendem este evento e dividimos pelo número total de possibilidades. Por exemplo, a probabilidade de rolar um 3 em um dado só é atendida pelo número 3. Entretanto, temos 6 possibilidades em um dado, os números que vão de 1 a 6 (o 3 inclusive). Desta forma, temos uma possibilidade que atende ao evento desejado dividido por 6 possibilidades no total, ou 1/6. Se quisermos saber a probabilidade de tirar um número menor que 3, este evento
Eventos dependentes e independentes
Um primeiro conceito importante da Probabilidade é o conceito de eventos dependentes e independentes.
Os eventos independentes são eventos nos quais saber o resultado de um deles não nos dá qualquer informação sobre o possível resultado do segundo. O rolar de um dado não nos dirá nada sobre o resultado do rolar do segundo dado.
Analogamente, eventos dependentes são eventos nos quais o resultado de um nos dá mais informações sobre a probabilidade do outro. Neste caso, o rolar de um dado nos dá informações se queremos saber a probabilidade, por exemplo, de rolar 6 em dois dados.
Para eventos independentes, a probabilidade de dois eventos acontecerem é igual a probabilidade de um multiplicada pela probabilidade do outro. Desta forma, se a probabilidade de rolar um determinado valor no dado é de 1/6, a probabilidade de rolar dois 6 seguidos é calculada da seguinte forma:
Sendo P(A) a probabilidade do evento A, P(B) a probabilidade do evento B e P(A,B) a probabilidade de ocorrerem os eventos A e B:
`P(A,B) = P(A) × P(B)
probability_of_6 = 1/6
# Probabilidade de rolar dois 6 em dois dados
print(probability_of_6 * probability_of_6)
0.027777777777777776Esta é a probabilidade de dois dados rolarem 6 seguidamente. Vamos usar a função Fraction do pacote fractions, para mostrar que este número equivale a 1/36, que é exatamente o resultado em forma de fração de 1/6 multiplicado por 1/6:
# Utilizando Fraction para retornar o valor em forma de fração
from fractions import Fraction
print(Fraction(probability_of_6 * probability_of_6).limit_denominator())
1/36Evento Complementar
Eventos complementares são um conceito simples. Um evento complementar a um evento A é aquele que engloba todos os resultados que não atendem ao evento A. Novamente utilizando o rolar do dado como exemplo, se um evento A indica a probabilidade deste dado rolar um número menor ou igual a 2, que seria de 2/6, seu evento complementar seria a probabilidade do dado rolar um número maior que 2, ou 4/6. O cálculo da probabilidade de um evento complementar é bem simples, bastando subtrair de 1 a probabilidade do evento A. Como este cálculo é simples demais, então creio que não há necessidade de mostra-lo como código.
Este conceito pode ser útil em casos onde é mais fácil calcular a probabilidade do complementar do que do evento em si. Vejamos por exemplo, o seguinte exemplo. Qual a probabilidade de jogar dois dados e os dois números serem diferentes? Neste caso, a lista de resultados que atendem as condições entre os 36 possíveis são muitos. Mas o evento complementar deste é quando jogamos dois dados e os dois números rolados são iguais. Desta forma, os resultados que atendem a condição limitam-se a (1,1), (2,2), (3,3), (4,4), (5,5) e (6,6). Assim, podemos facilmente calcular a probabilidade do evento complementar em 6/36, e a probabilidade do evento desejada em 1 - 6/36, equivalente a 30/36 ou 5/6.
Eventos Mutuamente Exclusivos
Eventos mutuamente exclusivos ocorrem quando entre dois eventos, apenas um pode acontecer. Ao jogar uma moeda, ela tem que resultar em cara ou coroa. Os dois não podem acontecer simultaneamente. Em um dado, o número rolado tem que ser par ou ímpar. Nenhum número atende as duas condições simultaneamente.
Para dois eventos mutualmente exclusivos A e B, P(A,B), ou seja, a probabilidade que os dois ocorram, é igual a zero. Entretanto, podemos calcular a probabilidade de P(A ou B), que para estes tipos de eventos, será igual a P(A) + P(B). Para o caso dos dados, por exemplo, P(A ou B) será igual a 1, pois o número rolado necessariamente será par um ímpar. Para outro exemplo, em um baralho, consideremos a probabilidade de uma carta ser um valete (P(A)), igual a 4/52, ou 1/13, e a probabilidade dela ser um Ás (P(B)), também 1/13. Estas duas probabilidades dão-se por termos 4 de cada uma destas cartas em um baralho de 52 cartas. São eventos mutualmente exclusivos, pois uma carta não pode ser os dois. Desta forma, P(A,B) é igual a zero. Entretanto, a probabilidade dela ser um Valete ou um Ás (P(A ou B)) será igual à soma de P(A) e P(B), totalizando 1/13 + 1/13 = 2/13. Novamente, como são casos de matemática básica, não creio que haja necessidade de mostrá-los como código.
Probabilidade Condicional
Para eventos dependentes, o cálculo da Probabilidade muda. Vamos estabelecer que:
- P(A|B) -> Probabilidade condicional de A dado B, ou seja, probabilidade do evento A ocorrer, dado que ocorreu o evento B
- P(A,B) -> Como já vimos, é a probabilidade dos dois eventos ocorrerem
- P(A) e P(B) -> Também, como já vimos, é a probabilidade de cada evento acontecer
Para eventos dependentes, o cálculo é o seguinte:
P(A|B) = P(A,B)/P(B)
E algumas vezes, passamos P(B) para o outro lado da igualdade, e a equação fica assim:
P(A,B) = P(A|B) × P(B)
Vejamos um exemplo e um pouco de código. Consideremos um dado. Seja o primeiro evento tirar um número ímpar e o segundo tirar um 5 ou 6 no dado. Vamos calcular a probabilidade de A dado B.
P(A|B) = ??
P(A) = 3/6
P(B) = 2/6
P(A,B) = 2/6 × 3/6 = 0,16666 ou 16,66%, ou ainda 1/6 - Este resultado equivale a nossa única possibilidade, que é o número 5.
P(A|B) = (1/6)/(2/6)
Vejamos o código para chegar na resposta final:
# Probabilidade do evento A: dado ser ímpar
probabilidade_impar = 3/6
# Probabilidade do evento B: dado ser 5 ou 6
probabilidade_5_ou_6 = 2/6
# Probabilidade dos dois eventos
probabilidade_ambos = probabilidade_impar * probabilidade_5_ou_6
print(probabilidade_ambos)
0.16666666666666666
print(Fraction(probabilidade_ambos).limit_denominator())
1/6
# Probabilidade de A dado B igual a P(A,B) / P(B)
probabilidade_a_dado_b = probabilidade_ambos / probabilidade_5_ou_6
print(probabilidade_a_dado_b)
0.5
print(Fraction(probabilidade_a_dado_b).limit_denominator())
1/2Vamos interpretar alguns destes resultados. Primeiramente, no cálculo da probabilidade de ambos os eventos, chegamos a um resultado de 1/6. Analisemos os dois eventos em separado. No caso do evento A, a probabilidade de um dado tirar um número ímpar, os resultados que atendem esta condição são os números 1, 3 e 5. Para o evento B, tirar um 5 ou um 6, os resultados que atendem, obviamente, são o 5 e o 6. Analisando conjuntamente, o único número que atende os dois eventos é o 5. Logo, 1/6, a chance de tirar um cinco no dado.
Agora, analisemos a probabilidade de A dado B. Considerando que B aconteceu, sabemos que o número rolado é 5 ou 6. O resultado entre estes que atende o evento A é o 5. Dentro do universo de possibilidades de B, temos um resultado que atende nossa condição entre dois possíveis. Logo, 1/2. Assim, também comprovamos que os eventos são independentes, pois o cálculo de P(A,B) leva a uma conclusão que confere com a realidade de cada evento.
Vamos calcular e analisar rapidamente a probabilidade P(B|A):
probabilidade_b_dado_a = probabilidade_ambos / probabilidade_impar
print(probabilidade_b_dado_a)
0.3333333333333333
print(Fraction(probabilidade_b_dado_a).limit_denominator())
1/3Neste caso, sabemos que o evento A, o dado rolar um número ímpar, já ocorreu. Então, temos 1, 3 ou 5. Entre estes, o único número que atende a condição do evento B, rolar um 5 ou um 6, é o próprio 5. Desta forma, dentre os 3 possíveis resultados A, apenas um atende a condição B, levando desta forma a uma probabilidade de B dado A igual a 1/3.
Teorema de Bayes
O Teorema de Bayes é um conceito importantíssimo da probabilidade e uma das ferramentas mais importantes de serem aprendidas para um Cientista de Dados. Este já foi usado em diversas aplicações reais, como por exemplo a classificação de um email como spam ou não. O Teorema de Bayes é uma forma calcular probabilidades condicionais de forma reversa.
Vamos considerar o clássico exemplo para explicar o teorema. Temos uma determinada doença A, e um teste T utilizado para detectar esta doença. O teste não é 100% confiável, indicando pessoas que não tem a doença como doentes (falsos positivos) e não detectando a doença em pessoas que a possuem (falsos negativos). Consideremos que 1% das pessoas possui esta doença e, logo, 99% das pessoas não a possui. O teste detecta a doença em pessoas efetivamente doentes 90% das vezes e, consequentemente, não detecta a doença em pessoas doentes em 10% dos casos. Em pessoas não doentes, o teste detecta a doença (erradamente) em 5% dos casos e não detecta em 95% dos casos. Podemos resumir desta forma:
| Pessoa Doente (1%) | Pessoa não doente (99%) | |
|---|---|---|
| Teste positivo | 90% | 5% |
| Teste negativo | 10% | 95% |
Agora, vamos supor que você fez o teste e o resultado deu positivo. Como devemos interpretar este resultado? Obviamente, existe uma chance de você possuir a doença e uma chance de não possuir. A chance de você ter a doença e o teste detecta-la (verdadeiro positivo) é igual a chance de você ter a doença multiplicado pela chance do teste ter dado positivo corretamente. Analogamente, a chance de você não ter a doença e o teste detecta-la mesmo assim (falso positivo) é igual a chance de você não ter a doença multiplicado pela chance do teste ter dado positivo incorretamente, e assim por diante, para todos os resultados. Atualizamos então a tabela, que fica assim:
| Pessoa Doente (1%) | Pessoa não doente (99%) | |
|---|---|---|
| Teste positivo | Prob Doente e teste pos: 1% × 90% = 0,9% | Prob Não Doente e teste pos: 99% × 5% = 4,95% |
| Teste negativo | Prob Doente e teste neg: 1% × 10% = 0,1% | Prob Não Doente e teste neg: 99% × 95% = 94,05% |
Estas então são nossas probabilidades para cada evento. Note que, se somadas, o resultado é 1, ou 100%. Mas agora temos uma dúvida. Se nosso teste deu positivo, qual a chance de termos a doença? Considerando o cálculo básico de probabilidade, temos que a chance de ter a doença é igual à chance do evento desejado dividido por todas as possibilidades. O evento desejado é um positivo verdadeiro, ou seja, teste positivo e a pessoa com doença. Para este caso, a probabilidade é de 0,9%. O total de possibilidades com relação ao teste positivo seria a soma da probabilidade de “Doente e teste pos” (verdadeiro positivo) com “Não Doente e teste pos” (falso positivo), que resultará em 0,9% + 4,95%, igual a 5,85%. Fazendo toda a conta então, nossa chance de ter a doença se temos um teste positivo é de 0,9%/5,85% = 0.1538, ou 15,38%. É uma chance bem mais baixa do que imaginamos apenas ao olhar para o problema e para a suposta precisão do teste.
Considerando o seguinte:
P(D|A) = Probabilidade de ter a doença dado um teste positivo (este é a probabilidade que desejamos saber)
P(D) = Probabilidade da pessoa ter a doença = 1%
P(A|D) = Probabilidade de um teste positivo se a pessoa tem a doença = 0,9% (
P(A|¬D) = Probabilidade de um teste positivo se a pessoa não tem a doença = 4,95%
P(¬D) = Probabilidade da pessoa não ter a doença = 99%
O Teorema de Bayes diz que:
Vamos ver um pouco de código para fazer estas contas e comprovar nosso resultado que chegamos ali em cima (15,38%):
# A probabilidade de uma pessoa ter certa doença A é de 1%
# consequentemente, a probabilidade de não ter a doença é de 99%
probabilidade_doenca = 0.01
probabilidade_nao_doenca = 1 - probabilidade_doenca
# Um teste T para detectar a doença não é 100% confiável, detectando
# a doença em pessoas não doentes e não detectando em pessoas doentes
# O teste detecta a doença em pessoas doentes em 90% dos casos
# e não detecta a doença em pessoas doentes em 10% dos casos
prob_teste_pos_e_doenca = 0.9
prob_teste_neg_e_doenca = 0.1
# O teste detecta a doença em pessoas não doentes em 5% dos casos
# e não detecta a doença em pessoas não doentes em 95% dos casos
prob_teste_pos_e_nao_doenca = 0.05
prob_teste_neg_e_nao_doenca = 0.95
# Verdadeiro positivo: chance de ter a doença e o teste dar positivo
prob_verdadeiro_positivo = probabilidade_doenca * prob_teste_pos_e_doenca
# Verdadeiro negativo: chance de não ter a doença e o teste dar negativo
prob_verdadeiro_negativo = probabilidade_nao_doenca * prob_teste_neg_e_nao_doenca
# Falso positivo: chance de não ter a doença e o teste dar positivo
prob_falso_positivo = probabilidade_nao_doenca * prob_teste_pos_e_nao_doenca
# Falso negativo: chance de ter a doença e o teste dar negativo
prob_falso_negativo = probabilidade_doenca * prob_teste_neg_e_doenca
# Fizemos o teste e o resultado foi positivo. Qual a chance de eu ter a doença?
# Teorema de Bayes: P(D|A) = (P(A|D) * P(D)) / (P(A|D) * P(D) + P(A|¬D) * P(¬D))
# P(D|A) = Probabilidade de doença dado um teste positivo. É o que desejamos calcular
# P(A|D) = Probabilidade do teste ser positivo se você tem a doença -> 90%
# P(D) = Probabilidade de ter a doença -> 1%
# P(A|¬D) = Probabilidade do teste ser positivo e você não ter a doença -> 5%
# P(¬D) = Probabilidade de não ter a doença -> 99%
# Simplificar as variáveis para que a equação não fique muito extensa
P_A_D = prob_teste_pos_e_doenca
P_D = probabilidade_doenca
P_A_ND = prob_teste_pos_e_nao_doenca
P_ND = probabilidade_nao_doenca
prob_doente_dado_positivo = (P_A_D * P_D) / (P_A_D * P_D + P_A_ND * P_ND)
print(prob_doente_dado_positivo)
0.15384615384615385E assim, podemos calcular as probabilidades de forma reversa, como falamos anteriormente. O Teorema é útil para calcular as probabilidades reais nestes casos. No caso do filtro de spam, para dar um exemplo mais real, as probabilidades se alteram para a probabilidade de um email que seja spam ter determinadas palavras, e as chances de um email que não seja spam conter a mesma palavra. Para um artigo mais completo sobre isso, veja aqui no Wikipedia.
Por enquanto é isso. Acredito que as partes mais básicas e importantes foram faladas aqui. Faltaram distribuições e o teorema central do limite, que falaremos em um post posterior.
Abraços!